سلام 

من بعد از مدتها میخوام دوباره یه مطلب در مورد پایتخت ایران بنویسم

چند وقت پیش توی صحن مجلس بحث انتقال پایتخت مطرح شد.متاسفانه و صد متاسفانه نمیدونم این خبرنگارا چرا اینجوری حرف میزنن.هرچیزی رو که باهاش به هر دلیلی(که واقعا نمیدونم چیه) مخالفن با مسخره کردن یا جبهه گرفتن و . خراب می کنن.

طرح تو چند وقت تو صحن مجلس بود و بحث انتقال به یه شهر دیگه مثل سمنان یا. بود  اما خبرنگار

ابله و احمق(معذرت می خوام ولی واژه ای برازنده تر ازین پیدا نکردم.چون یا عمدی میگه یا سهوی)

میگه میخوایید پایتخت عوض بشه تا به شما هم بگن بچه تهران.آخه شما که سواد یک موضوع رو ندارید چرا اینجور قضاوت می کنید.یه نگاه به آمار مرگ و میر تهران بکنید.ببینید امار بهشت زهرا چند درصد مرگ در تهران رو بر اثر آلودگی اعلام می کنه؟؟؟

این شهر واقعا دیگه ظرفیت ندارهتوی مقاله قبلیم نوشتم و یه نظر سنجی هم گذاشتم.بالای 60 درصد از 220 نفر شرکت کننده موافق انتقال پایتخت بودن(البته یه نمونه کوچیک و آماری)

دلایل عمده خودم هم گفتم(پیشرفت سایر استانها-دوری از حاشیه نشینی-کاهش هزینه های احداث زیربناهایی مثل تونل و مترو و پل و .-کاهش مرگ و میر که متاسفانه جزو معدود چیزهایی هست در ایران که ارزون تر میشه-گسترش عدالت --- دیگه لااقل هوا بدتر ازین نمیشه-خود مردم تمایل پیدا می کنن ازینجا برن اگه دولت بره یه شهر که بخوا اونجا رو رشد بده-فقط مسئله تامین امنیت و زیربناهای اون شهر میمونه که یه ضرر و فایده کنید می بینید تو بلند مدت(مثلا 5 الی 10 سال ) کدوم به نفع کشور و مردم(نه دولت و حکومت) هستو .

به قول امام خمینی :به داد اسلام برسید

منم میگم به داد مردم برسید.یکی دلسوز تو مسئولان نیستآیا؟؟؟؟

مقدمه

در برنامه ریزی خطی می توان مسائل مختلف از قبیل ترکیب تولید ، سرمایه گذاری ، بازار یابی ، حمل و نقل ، فرمولاسیون محصول ، زمان بندی چند دوره ای و . را مدل سازی کرده با استفاده از نرم افزارهای مربوطه به حل آن بپردازیم.

در این مقاله ضمن آموزش نرم افزار لینگو در قالب فلش، به حل نمونه ای از مسئله برنامه ریزی خطی پرداخته میشود.

 فرم عمومی برنامه ریزی خطی

1- تابع هدف Objective Function

ت و هدف از طرح مسئله است که در اغلب مسائل به صورت ماکسیمم (حداکثر سود ، بازدهی و .) و در برخی موارد (مانند حداقل هزینه ) این تابع مینیمم در نظر گرفته می شود.


2- متغیر های تصمیم Decision Variable 

متغیر هایی هستند که تاثیر مستقیم بر تابع هدف دارند و محدودیتها بر اساس آنها لحاظ می گردد. انتخاب متغیرهای تصمیم برای حل مدل برنامه ریزی خطی بسیار حائز اهمیت می باشد.
متغیر های تصمیم غالبا به صورت غیر منفی در نظر گرفته می شوند و در برخی موارد نیز می توانند آزاد در علامت ( غیر مثبت ) باشند.



3- محدودیت ها Constraints
شامل محدودیتها و ت های مختلفی است که جهت تحقق تابع هدف با استفاده از متغیر های تصمیم درنظر گرفته می شود .


تعاریف مختلف

- جواب :
 کلیه مقادیری که متغیرهای تصمیم اختیار میکنند به تنهایی یک جواب محسوب می شوند.

- جواب موجه :
جوابی است که در تمام محدودیت ها صدق می کند.

- منطقه موجه :
ناحیه ای از جواب های موجه است که در همه محدودیت ها صادق است.

- جواب غیر موجه :
کلیه مقادیری که خارج از منطقه موجه قرار دارند.

- جواب بهینه :
جوابی است که به ازای آن مقدار تابع هدف مطلوب ترین و بهینه ترین وضعیت خود را داراست. ( برای تابع هدف ماکسیمم ، جواب هایی که تابع را حد اکثر و برای مینیمم ، حداقل کنند  )
به عبارتی دیگر هر یک از جواب های بهینه مشخص می کند که از هر متغیر تصمیم چه تعداد (مقدار )  تخصیص یابد تا تابع هدف ماکسیمم یا مینیمم شود .

جواب های بهینه اصلی ترین  هدف تشکیل مدل برنامه ریزی خطی است .

قابل ذکر است نرم افزار لینگو ( که فایل آموزش آن در این مقاله ضمیمه شده است ) ، جواب های بهینه را در اختیار ما قرار میدهد.


- جواب های بهینه مدل برنامه ریزی خطی ، ممکن است انواع مختلفی داشته باشند که به شرح ذیل بیان می گردد

الف : جواب بهینه چند گانه داشته باشد:
ممکن است بیش از یک جواب موجه مقدار تابع هدف را مطلوب ترین نماید که در این صورت همه ی آنها جواب بهینه خواهند بود .

ب : فاقد جواب بهینه باشد :
در این حالت مدل جواب بهینه ندارد و این در واقعیت امکان پذیر نیست ، در چنین صورتی باید مجددا مسئله را فرموله و حل نماییم .
 
ج: ناحیه جواب ، بی کران باشد :
چنانچه با این حالت مواجه شویم باید بر مشاهده و تعریف مدل بازنگری کنیم که قطعا اشتباهی رخ داده و باید رفع شود .




4 - متغیر های کمکی

از آنجا که مدودیت ها در مدل باید بصورت تساوی باشند ، لذا برای استاندارد کردن آنها  از متغیر های کمکی استفاده می شود که بر دو نوع است :


Slack Variable 1-4 متغیرهای لنگی
 برای استاندارد کردن محدودیت هایی که به صورت کوچکتر یا مساویند استفاده می شود . متغیر های لنگی همواره بزرگتر از صفرند.


Artificial Variable 2-4 متغیرهای مصنوعی
برای استاندارد سازی محدودیت های تساوی ( به محدودیت افزوده میشوند ) و محدودیت های بزگتر مساوی ( یک لنگی اضاف و یک مصنوعی از محدودیت کاسته) ،استفاده می شوند .

گفتنی است متغیر های کمکی فقط در محاسبات دستی کاربرد دارند و محاسبات نرم اقاری خود به خود لحاظ می شود .


 
بعد از آن که مسئله مورد نظر را با رعایت فرم عمومی مدل برنامه ریزی خطی فرموله کردیم ، حاصل را در نرم افزارهای مربوطه وارد کرده و جواب های بهینه را استخراج میکنیم . 


حل یک مسئله نمونه با استفاده از نرم افزار لینگو :

صورت مسئله :
شرکتی مونتاژ محصول را که شامل قاب – میله فی و بلبرینگ است ، برعهده دارد . شرکت میله ی فی و قاب را تولید می کند و بلبرینگ را از تولید کننده دیگری خریداری می کند ، هر میله ی فی باید مراحل ماشین سندان ، ماشین تراش و ماشین تبزکن را بگذراند ، این مراحل به ترتیب 1/2 ساعت ، 0/2 ساعت و 0/3 ساعت برای هر میله ی فی وقت می گیرد . هر قاب نیز 0/8 ساعت در ماشین سندان ، 0/1 ساعت در ماشین سوراخ کننده ، 0/3 ساعت در آسیاب و 0/5 ساعت در ماشین تبزکن ، وقت می گیرد .
شرکت 5 ماشین تراش ، 10 ماشین تیزکن ، 20 ماشین سندان و 3 ماشین سوراخکن و 6  آسیاب دارد ، برآورد شده است هر ماشین ماکزیمم 2400 ساعت در هر سال کار می کند .
مسئله را برای ماکزیمم تعداد مولفه های محصول تولید به مونتاژ حل می کنیم .
 
 


حل مسئله :

گام اول : انتخاب متغیر های تصمیم 
A : تعداد میله فی که در یک سال باید تولید شود
B : تعداد قاب که در یک سال باید تولید شود د


گام دوم : محاسبات لازم
ماکزیمم ساعت کار 20 ماشین سندان در یکسال              48000= 20 * 2400
ماکزیمم ساعت کار 5 ماشین تراش در یکسال                   12000= 5 * 2400                   
ماکزیمم ساعت کار 10 ماشین تیز کن در یکسال              24000= 10 * 2400  
ماکزیمم ساعت کار 3 ماشین تراش در یکسال                   12000= 3 * 2400      
ماکزیمم ساعت کار 6 ماشین آسیاب در یکسال                 14400= 6 * 2400                   
            
                


گام سوم :  تشکیل تابع هدف

گام چهار : شروع کار با نرم افزار


مدل تایپ شده زیر را عینا در نرم افزار تایپ می کنیم .

 می توانید فایل آموزش Lingo 10.0 را از لینک های زیر دانلود نمایید
( فایل های آموزشی فوق توسط اینجانب به صورت کاملا مالتی مدیا در قالب فلش تهیه گردیده است .)

نکته مهم : 

همانطور که گفته شد ، دروس ارائه شده درقالب فایل Flash میباشند ، لذا برای مشاهده آنها بعد از خارج کردن فایل دانلودی از حالت فشرده ( با استفاده از نرم افزار Win RAR ) می بایست از نرم افزار Flash Player استفاده نمایید.

درس اول : آشنایی با نوار ابزار و گزینه های مهم در لینگو

فرمت فایل دانلودی : Zip ، بعد از دانلود آنرا از حالت فشرده در بیاورید .

سایز فایل دانلودی: 1.72 MB

درس دوم : اصول وارد کردن اطلاعات و مدل مورد نظر 

فرمت فایل دانلودی : Zip ، بعد از دانلود آنرا از حالت فشرده در بیاورید .

سایز فایل دانلودی: 1.48 MB

درس سوم : اعمال تنظیمات روی مدل و دریافت جواب های بهینه  

فرمت فایل دانلودی : Zip ، بعد از دانلود آنرا از حالت فشرده در بیاورید .

سایز فایل دانلودی: 1.65 MB

دانلود درس سوم ( رمز فایل : inen.mihanblog.com )

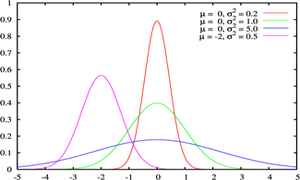
منحنی رفتار این تابع تا حد زیادی شبیه به زنگ های کلیسا می باشد و به همین دلیل به آن Bell Shaped هم گفته میشود. با وجود اینکه ممکن است ارتفاع و نحوه انحنای انواع مختلف این منحنی یکسان نباشد اما همه آنها یک ویژگی یکسان دارند و آن مساحت واحد می باشد.
ارتفاع این منحنی با مقادیر میانگین (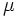) و انحراف معیار() ارتباط دارد. با وجود فرمول نسبتا" پیچیده و دخیل بودن پارامترهای ثابتی چون عدد (p) یا عدد (e) در این فرمول، می توان از آن برای مدل کردن رفتار میزان IQ، قد یا وزن انسان، پراکندگی ستارگان در فضا و . استفاده کرد.

تابع چگالی احتمال

تابع چگالی احتمال برای توزیع نرمال بر حسب امید ریاضی و واریانس تعریف میشود.و تابع آن به صورت زیر است:

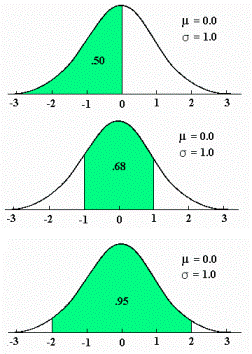
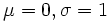اگر در این فرمول باشد در این صورت به آن تابع توزیع نرمال استاندارد گویند. در این حالت تابع توزیع به صورت زیر خواهد بود:

 

 

 

پارامترها	μ مکان (حقیقی) σ2 > 0 یه توان دو مقیاس (حقیقی)
‫گستره
تابع چگالی‌ احتمال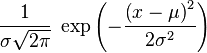
تابع توزیع تجمعی‫(سی‌دی‌اف)
میانگین	μ
میانه	μ
مُد	μ
واریانس	σ2
چولگی	0
کشیدگی	0
انتروپی
‫تابع مولد گشتاور (ام جی اف)
تابع مشخصه

امروز با یک وبلاگی از بچه های الکترونیک آشنا شدم که خیلی خوب متلب رو به صورت خلاصه و کاربردی توضیح داده بود.اکثریت رشته ها با برنامه نویسی در متلب سروکار دارند.بچه های صنایع هم جزو همونا.مخصوصا برای برنامه نویسی در الگوریتم های فراابتکاری مورد نیازتون میشه.حتما سر بزنید.اینم آدرسش:

http://matlabseven.blogfa.com

امروز براتون می خوام یه فایل پاور پوینت بزارم که توضیحاتی در مورد PSO یا همون الگوریتم جامعه پرندگان می ده.

فایل کد اون رو هم قرار دادم.در ضمن پاورپوینتش به صورت فارسی می باشد.